Bias and Variance

Question

In the first half of the exercise, you will implement regularized linear regression to predict the amount of water flowing out of a dam using the change of water level in a reservoir. In the next half, you will go through some diagnostics of debugging learning algorithms and examine the effects of bias and variance.

理论基础

我们在训练模型时通常准备训练集，验证集和测试集三组数据。训练集负责提供数据进行训练，验证集负责对训练结果进行评价并反馈修改意见，测试集体现最终的一个预测能力。偏差主要体现为训练后模型与训练集中数据的偏离程度，偏差越小代表与训练集数据拟合越好（太小会导致过拟合）。方差体现为训练后模型加入验证集数据后，预测结果与验证集数据的偏离程度，我们也需要使方差在一定程度上尽可能小，使得我们测试集中的预测结果不会偏离真实结果太多。这里X将从最基本的一次线性函数开始，通过绘图直观展示特征化、归一化、正则化、增加数据数量等手段对于模型及其偏差、方差的影响。

数据读取处理

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
from scipy.optimize import minimize

data=loadmat('Bias and Variance.mat')
data.keys()
dict_keys(['__header__', '__version__', '__globals__', 'X', 'y', 'Xtest', 'ytest', 'Xval', 'yval'])

X_train,y_train=data['X'],data['y']
X_train.shape,y_train.shape
((12, 1), (12, 1))

X_val,y_val=data['Xval'],data['yval']
X_val.shape,y_val.shape
((21, 1), (21, 1))

X_test,y_test=data['Xtest'],data['ytest']
X_test.shape,y_test.shape
((21, 1), (21, 1))

X_train=np.insert(X_train,0,1,axis=1)
X_val=np.insert(X_val,0,1,axis=1)
X_test=np.insert(X_test,0,1,axis=1)

def plot_data():
    fig,ax=plt.subplots()
    ax.scatter(X_train[:,1],y_train)
    ax.set(xlabel='change in water level(x)',ylabel='water flowing out of the dam(y)')

plot_data()

​

​

def reg_cost(theta,X,y,lamda):
    
    cost=np.sum(np.power((X@theta-y.flatten()),2))
    reg=theta[1:]@theta[1:]*lamda
    
    return (cost+reg)/(2*len(X))

theta=np.ones(X_train.shape[1])
lamda=1
reg_cost(theta,X_train,y_train,lamda)
303.9931922202643

def reg_gradient(theta,X,y,lamda):
    
    grad=(X@theta-y.flatten())@X
    reg=lamda*theta
    reg[0]=0
    
    return (grad+reg)/len(X)

reg_gradient(theta,X_train,y_train,lamda)
array([-15.30301567, 598.25074417])

def train_model(X,y,lamda):
    
    theta=np.ones(X.shape[1])
    res=minimize(fun=reg_cost,x0=theta,args=(X,y,lamda),method='TNC',jac=reg_gradient)
    
    return res.x

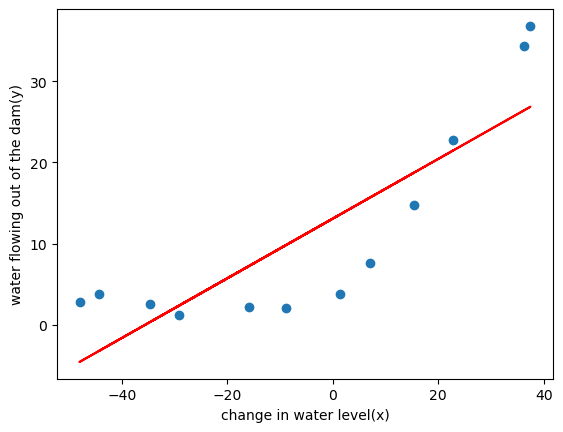
普通的一次线性

theta_final=train_model(X_train,y_train,lamda=0)

plot_data()
plt.plot(X_train[:,1],X_train@theta_final,c='r')
plt.show()

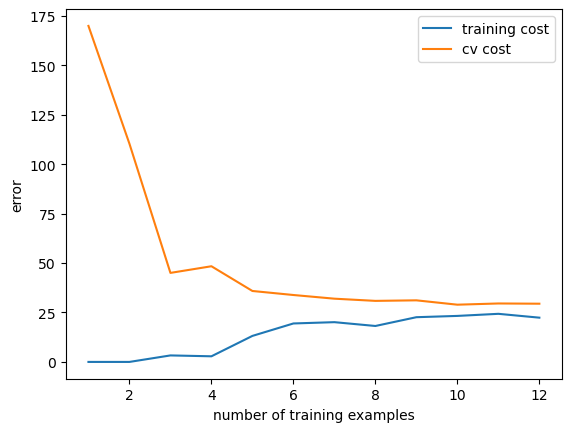
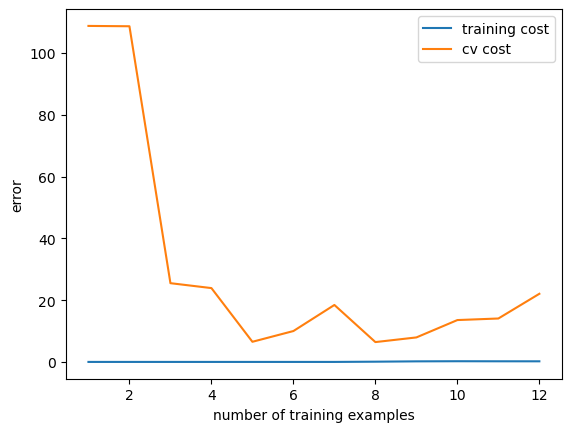
偏差方差随数据增多的变化图

def plot_learning_curve(X_train,y_train,X_val,y_val,lamda):
    
    x=range(1,len(X_train)+1)
    training_cost=[]
    cv_cost=[]
    
    for i in x:
        res=train_model(X_train[:i,:],y_train[:i,:],lamda)
        training_cost_i=reg_cost(res,X_train[:i,:],y_train[:i,:],lamda)
        cv_cost_i=reg_cost(res,X_val,y_val,lamda)
        training_cost.append(training_cost_i)
        cv_cost.append(cv_cost_i)
        
    plt.plot(x,training_cost,label='training cost')
    plt.plot(x,cv_cost,label='cv cost')
    plt.legend()
    plt.xlabel('number of training examples')
    plt.ylabel('error')
    plt.show()

plot_learning_curve(X_train,y_train,X_val,y_val,0)

​

​

将X特征化和归一化

def poly_feature(X,power):
    
    for i in range(2,power+1):
        X=np.insert(X,X.shape[1],np.power(X[:,1],i),axis=1)
    return X

def get_means_stds(X):
    
    means=np.mean(X,axis=0)
    stds=np.std(X,axis=0)
    return means,stds

def feature_normalize(X,means,stds):
    
    X[:,1:]=(X[:,1:]-means[1:])/stds[1:]
    
    return X

power=6

X_train_poly=poly_feature(X_train,power)
X_val_poly=poly_feature(X_val,power)
X_test_poly=poly_feature(X_test,power)

train_means,train_stds=get_means_stds(X_train_poly)

X_train_norm=feature_normalize(X_train_poly,train_means,train_stds)
X_val_norm=feature_normalize(X_val_poly,train_means,train_stds)
X_test_norm=feature_normalize(X_test_poly,train_means,train_stds)

theta_fit=train_model(X_train_norm,y_train,lamda=0)

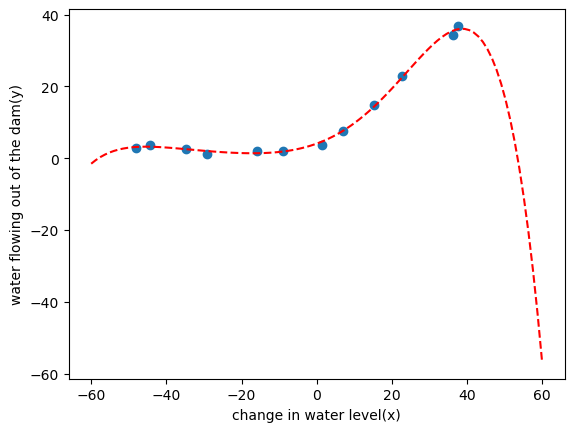
def plot_poly_fit():
    plot_data()
    x=np.linspace(-60,60,100)
    xx=x.reshape(100,1)
    xx=np.insert(xx,0,1,axis=1)
    xx=poly_feature(xx,power)
    xx=feature_normalize(xx,train_means,train_stds)
    
    plt.plot(x,xx@theta_fit,'r--')

plot_poly_fit()

​

​

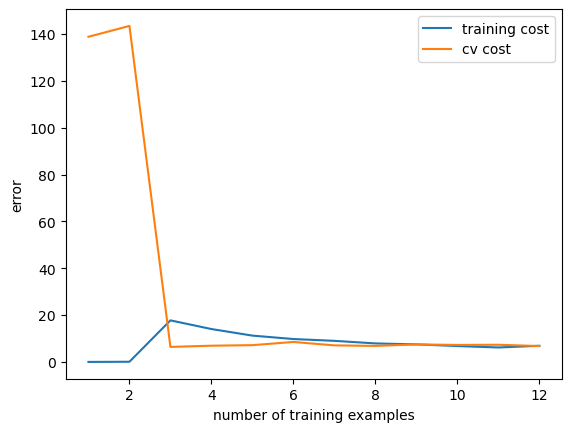
plot_learning_curve(X_train_norm,y_train,X_val_norm,y_val,lamda=0)

​

​

这里发现随数据的增多偏差恒为0，且模型最终曲线具有特殊性，属于过拟合的情况，加入正则化手段防止其过拟合。

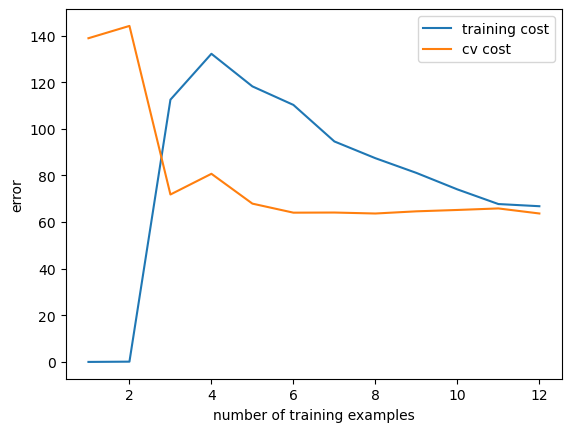
正则化

lambda=1

plot_learning_curve(X_train_norm,y_train,X_val_norm,y_val,lamda=1)

​

​

lambda=100

plot_learning_curve(X_train_norm,y_train,X_val_norm,y_val,lamda=100)

​

​

为正则化找到最合适的lambda

lamdas=[0,0.001,0.003,0.01,0.03,0.1,0.3,1,3,10]

training_cost=[]
cv_cost=[]

for lamda in lamdas:
    res=train_model(X_train_norm,y_train,lamda)
    
    tc=reg_cost(res,X_train_norm,y_train,lamda=0)
    cv=reg_cost(res,X_val_norm,y_val,lamda=0)
    
    training_cost.append(tc)
    cv_cost.append(cv)

plt.plot(lamdas,training_cost,label='training cost')
plt.plot(lamdas,cv_cost,label='cv cost')
plt.legend()
plt.show()

​

​

方差最小对应的lambda为

lamdas[np.argmin(cv_cost)]
3

根据图像，将此时的lambda视为最优参数，最终测试集的损失函数值为

res=train_model(X_train_norm,y_train,lamda=3)
test_cost=reg_cost(res,X_test_norm,y_test,lamda=0)
print(test_cost)

4.3976161577441975

Site

代码(Jupyter)和所用数据：https://github.com/codeYu233/Study/tree/main/Bias%20and%20Variance

Note

该题与数据集均来源于Coursera上斯坦福大学的吴恩达老师机器学习的习题作业，学习交流用，如有不妥，立马删除