Logistic Regression_2 Question Suppose you are the product manager of the factory and you have the test results for some microchips on two different tests. From these two tests, you would like to determine whether the microchips should be accepted or rejected.
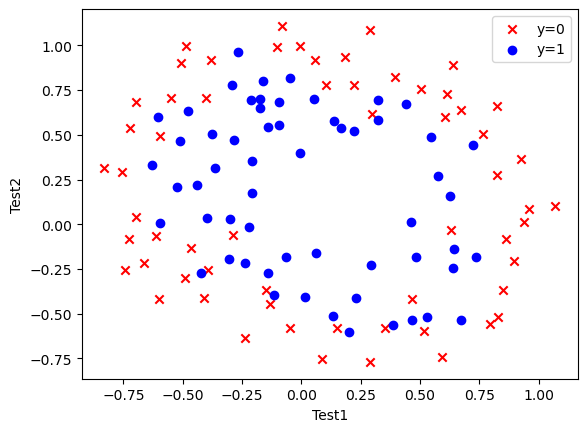
理论基础 跟文章Logistic Regression_1中的思路一样,我们需要进行分类预测。最简单的逻辑回归只需画一条线就能完成分类,这工作交给人来也能完成,并没有怎么很好体现机器学习的作用(如上一篇所示)。但是当我们导入工厂数据并绘制散点图后会发现事情并不是画一条线那么简单了。
这次我们初步估计需要画一个椭圆来进行分界。一次的线性方程已经不能满足需求,我们需要将f(X)扩展到更高次。以本题需用到的六次为例:
因此,我们需要采取手段来避免这种过拟合。最简单的方法当然是获取更多的训练数据,只要数据够多,就足以能反应潜在规律,拟合后的函数也就越精确。但现实我们肯定不容易得到那么多的数据。因此我们需要对参数向量Theta进行一定的约束操作。参数越多,参数越大越杂,过拟合越容易发生,因此我们可以引入一个惩罚项加入损失函数来完成对参数大小的限制,从而避免过度拟合。这也叫做正则化,这里采用的是L2正则。
数据读取处理 1 2 3 4 5 6 7 import numpy as np import pandas as pd import matplotlib.pyplot as plt path='Logistic Regression_2.txt' data=pd.read_csv(path,names=['Test1','Test2','Accepted']) data.head()
Test1
Test2
Accepted
0
0.051267
0.69956
1
1
-0.092742
0.68494
1
2
-0.213710
0.69225
1
3
-0.375000
0.50219
1
4
-0.513250
0.46564
1
1 2 3 4 5 6 fig,ax=plt.subplots() ax.scatter(data[data['Accepted' ]==0 ]['Test1' ],data[data['Accepted' ]==0 ]['Test2' ],c='r' ,marker='x' ,label='y=0' ) ax.scatter(data[data['Accepted' ]==1 ]['Test1' ],data[data['Accepted' ]==1 ]['Test2' ],c='b' ,marker='o' ,label='y=1' ) ax.legend() ax.set (xlabel='Test1' ,ylabel='Test2' ) plt.show()
特征映射 1 2 3 4 5 6 7 8 def feature_mapping (x1,x2,power ): data={} for i in np.arange(power+1 ): for j in np.arange(i+1 ): data['F{}{}' .format (i-j,j)]=np.power(x1,i-j)*np.power(x2,j) return pd.DataFrame(data)
1 2 3 4 5 6 x1=data['Test1'] x2=data['Test2'] data2=feature_mapping(x1,x2,6) data2.head()
F00
F10
F01
F20
F11
F02
F30
F21
F12
F03
...
F23
F14
F05
F60
F51
F42
F33
F24
F15
F06
0
1.0
0.051267
0.69956
0.002628
0.035864
0.489384
0.000135
0.001839
0.025089
0.342354
...
0.000900
0.012278
0.167542
1.815630e-08
2.477505e-07
0.000003
0.000046
0.000629
0.008589
0.117206
1
1.0
-0.092742
0.68494
0.008601
-0.063523
0.469143
-0.000798
0.005891
-0.043509
0.321335
...
0.002764
-0.020412
0.150752
6.362953e-07
-4.699318e-06
0.000035
-0.000256
0.001893
-0.013981
0.103256
2
1.0
-0.213710
0.69225
0.045672
-0.147941
0.479210
-0.009761
0.031616
-0.102412
0.331733
...
0.015151
-0.049077
0.158970
9.526844e-05
-3.085938e-04
0.001000
-0.003238
0.010488
-0.033973
0.110047
3
1.0
-0.375000
0.50219
0.140625
-0.188321
0.252195
-0.052734
0.070620
-0.094573
0.126650
...
0.017810
-0.023851
0.031940
2.780914e-03
-3.724126e-03
0.004987
-0.006679
0.008944
-0.011978
0.016040
4
1.0
-0.513250
0.46564
0.263426
-0.238990
0.216821
-0.135203
0.122661
-0.111283
0.100960
...
0.026596
-0.024128
0.021890
1.827990e-02
-1.658422e-02
0.015046
-0.013650
0.012384
-0.011235
0.010193
5 rows × 28 columns
1 2 3 4 X=data2.values X.shape (118, 28)
1 2 3 4 5 y=data.iloc[:,-1].values y=y.reshape(len(y),1) y.shape (118, 1)
损失函数 1 2 def sigmoid (z ): return 1 /(1 +np.exp(-z))
1 2 3 4 5 6 7 8 def costFunction (X,y,theta,lr ): A=sigmoid(X@theta) first=y*np.log(A) second=(1 -y)*np.log(1 -A) reg=np.sum (np.power(theta[1 :],2 ))*(lr/(2 *len (X))) return -np.sum (first + second)/len (X)+reg
1 2 3 4 theta=np.zeros((28,1)) theta.shape (28, 1)
1 2 3 4 5 lamda=1 cost_init=costFunction(X,y,theta,lamda) print(cost_init) 0.6931471805599454
梯度下降函数 costs是用来记录记录每次下降后的损失函数大小的,可以将其进行绘图或打印,观察模型梯度下降的效果如何。该程序没有进行展示。
1 2 3 4 5 6 7 8 9 10 11 12 13 def gradientDescent (X,y,theta,alpha,iters,lamda ): costs=[] for i in range (iters): reg=theta[1 :]*(lamda/len (X)) reg=np.insert(reg,0 ,values=0 ,axis=0 ) theta=theta - (X.T@(sigmoid(X@theta)-y))*alpha/len (X)-reg cost=costFunction(X,y,theta,lamda) costs.append(cost) return theta,costs
1 2 3 4 5 alpha=0.001 iters=200000 lamda=0.001 theta_final,costs=gradientDescent(X,y,theta,alpha,iters,lamda)
预测结果准确率 1 2 3 4 5 def predict (X,theta ): prob=sigmoid(X@theta) return [1 if x>=0.5 else 0 for x in prob]
1 2 3 4 5 6 y_=np.array(predict(X,theta_final)) y_pre=y_.reshape(len(y_),1) acc = np.mean(y_pre==y) print(acc) 0.8305084745762712
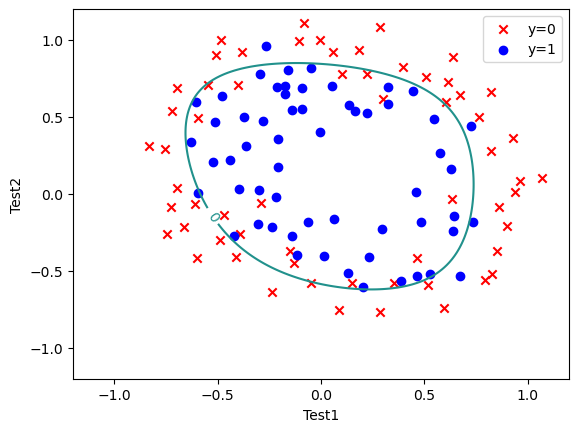
画图 1 2 3 4 5 6 7 8 9 10 11 12 13 14 x=np.linspace(-1.2 ,1.2 ,200 ) xx,yy=np.meshgrid(x,x) z=feature_mapping(xx.ravel(),yy.ravel(),6 ).values zz=z@theta_final zz=zz.reshape(xx.shape) fig,ax=plt.subplots() ax.scatter(data[data['Accepted' ]==0 ]['Test1' ],data[data['Accepted' ]==0 ]['Test2' ],c='r' ,marker='x' ,label='y=0' ) ax.scatter(data[data['Accepted' ]==1 ]['Test1' ],data[data['Accepted' ]==1 ]['Test2' ],c='b' ,marker='o' ,label='y=1' ) ax.legend() ax.set (xlabel='Test1' ,ylabel='Test2' ) cs=plt.contour(xx,yy,zz,0 ) plt.clabel(cs) plt.show()
Site 代码(Jupyter)和所用数据:https://github.com/codeYu233/Study/tree/main/Logistic%20Regression_2
Note 该题与数据集均来源于Coursera上斯坦福大学的吴恩达老师机器学习的习题作业,学习交流用,如有不妥,立马删除