Logistic Regression_1

Question

Suppose that you are the administrator of a university department and you want to determine each applicant’s chance of admission based on their results on two exams.

理论基础

最基本的逻辑回归底层依然是线性函数，同线性回归，有：
$$
f(x_{1},x_{2},x_{3},…,x_{n})=\theta_{0}+\theta_{1}x_{1}+…+\theta_{n}x_{n}
$$

$$
\begin{array}{}\Theta =\begin{bmatrix}
\theta_{0}\\
…\\
\theta_{n}
\end{bmatrix}\quad
X=\begin{bmatrix}1\\
x_{1}\\
…\\
x_{n}
\end{bmatrix}
\end{array}
$$

$$
f(x_{1},x_{2},x_{3},…,x_{n})=X^{T}\Theta
$$

逻辑回归作用是对数据进行分类，可以通过sigmoid函数将f（x）映射到0-1之间形成一个概率值，并与分界线0.5比较进行预测
$$
p(X)=\frac{1}{1+e^{-f(X)}}
$$

costfunction的构建：

该函数（交叉熵）鼓励将p（x）趋近于1的f（x）往正无穷进行训练，将p（x）趋近于0的f（x）往负无穷进行训练
$$
J(\Theta)= - \frac{1}{m} \sum_{i}^{m} (y_{i} ln{}^{p(X)} + (1 - y_{i}) ln{}^{(1-p(X))})
$$
梯度下降类似线性回归进行偏微分，结果为：

j=0时，x_j=1
$$
\theta_{j}=\theta_{j}-\frac{\alpha }{m}\sum_{i=1}^{m}(p(x^{i})-y^{i})x_{j}^{i}
$$
设定迭代次数进行循环，接收最终的theta，可得：
$$
p(X)=\frac{1}{1+e^{-（X^T\Theta）}}
$$

$$
\hat{y}=1 \quad if \quad p(X)>0.5 \quad else \quad \hat{y}=0
$$

数据读取处理

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

path='Logistic Regression_1.txt'
data=pd.read_csv(path,names=['Exam1','Exam2','Accepted'])
data.head()

	Exam1	Exam2	Accepted
0	34.623660	78.024693	0
1	30.286711	43.894998	0
2	35.847409	72.902198	0
3	60.182599	86.308552	1
4	79.032736	75.344376	1

fig,ax=plt.subplots()
ax.scatter(data[data['Accepted']==0]['Exam1'],data[data['Accepted']==0]['Exam2'],c='r',marker='x',label='y=0')
ax.scatter(data[data['Accepted']==1]['Exam1'],data[data['Accepted']==1]['Exam2'],c='b',marker='o',label='y=1')
ax.legend()
ax.set(xlabel='exam1',ylabel='exam2')
plt.show()

png

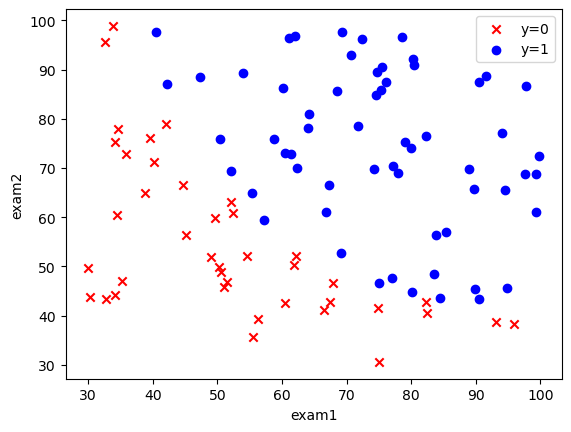
def get_Xy(data):
    
    data.insert(0,'ones',1)
    X_=data.iloc[:,0:-1]
    X=X_.values
    y_=data.iloc[:,-1]
    y=y_.values.reshape(len(y_),1)
    return X,y
X,y=get_Xy(data)
X.shape
(100, 3)

y.shape
(100, 1)

构造损失函数

1 2	def sigmoid(z): return 1/(1+np.exp(-z))

def costFunction(X,y,theta):
    
    A=sigmoid(X@theta)
    
    first=y*np.log(A)
    second=(1-y)*np.log(1-A)
    
    return -np.sum(first+second)/len(X)

theta=np.zeros((3,1))
theta.shape
(3, 1)

cost_init=costFunction(X,y,theta)
print(cost_init)

0.6931471805599453

构造梯度下降

def gradientDescent(X,y,theta,alpha,iters):
    m=len(X)
    costs=[]
    
    for i in range(iters):
        theta=theta-X.T@(sigmoid(X@theta)-y)*alpha/m
        cost=costFunction(X,y,theta)
        costs.append(cost)
        if i%1000==0:
            print(cost)
    return costs,theta

迭代得到结果

alpha=0.004
iters=200000

costs,theta_final=gradientDescent(X,y,theta,alpha,iters)

theta_final
array([[-23.77288372],
       [  0.20687383],
       [  0.19997746]])

1
2
3

def predict(X,theta):
    prob=sigmoid(X@theta)
    return [1 if x>=0.5 else 0 for x in prob]

准确率预估

y_=np.array(predict(X,theta_final))
y_pre=y_.reshape(len(y_),1)

acc = np.mean(y_pre==y)

print(acc)
0.91

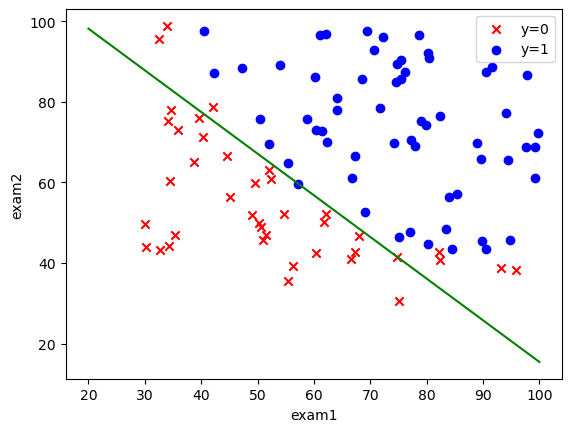
画图

coef1=-theta_final[0,0]/theta_final[2,0]
coef2=-theta_final[1,0]/theta_final[2,0]

x=np.linspace(20,100,100)
f=coef1+coef2*x

fig,ax=plt.subplots()
ax.scatter(data[data['Accepted']==0]['Exam1'],data[data['Accepted']==0]['Exam2'],c='r',marker='x',label='y=0')
ax.scatter(data[data['Accepted']==1]['Exam1'],data[data['Accepted']==1]['Exam2'],c='b',marker='o',label='y=1')
ax.legend()
ax.set(xlabel='exam1',ylabel='exam2')
ax.plot(x,f,c='g')
plt.show()