Linear Regression

Question

根据所提供的数据（房屋面积，卧室数量，房屋售价）通过基本的多元线性回归来进行机器学习拟合，从而实现对于已知面积和卧室数量的房屋的售价预测。

理论基础

多元线性方程可以表示为：

$$
f(x_{1},x_{2},x_{3},…,x_{n})=\theta_{0}+\theta_{1}x_{1}+…+\theta_{n}x_{n}
$$

将其参数与未知数向量化可得：

$$
\begin{array}{}
\Theta =\begin{bmatrix}
\theta_{0}\\
…\\
\theta_{n}
\end{bmatrix}\quad
X=\begin{bmatrix}1\\
x_{1}\\
…\\
x_{n}
\end{bmatrix}
\end{array}
$$

于是

$$
f(x_{1},x_{2},x_{3},…,x_{n})=X^{T}\Theta
$$

costfunction的建立：

m为训练集数据组数

$$
costfunction=\frac{1}{2m}\sum_{i=1}^{m}((X^{i})^{T}\Theta -y^{i})^{2}
$$

接下来是梯度下降：

将costfunction对于各参数theta求偏导，引入下降参数（决定每步按偏导率下降多少）alpha。注意因为theta0在式子中并没有与未知数x相乘，是一个“常数项”，所以与其他theta的梯度下降公式有所不同

$$
\begin{array}{}
\theta_{0}=\theta_{0}-\frac{\alpha }{m}\sum_{i=1}^{m}((X^{i})^{T}\Theta -y^{i})\\
.\\
.\\
.\\
\theta_{n}=\theta_{n}-\frac{\alpha }{m}\sum_{i=1}^{m}((X^{i})^{T}\Theta -y^{i})x_{n}^{i}
\end{array}
$$

设置恰当的循环次数进行梯度下降，并收集最终训练完成的theta，得到预测函数

$$
f_{final}(x_{1},x_{2},x_{3},…,x_{n})=X^{T}\Theta_{final}
$$

数据读取处理

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

data=pd.read_csv('Linear Regression_2.txt',names=['size','bedrooms','price'])
data_2=data
data.head()

	size	bedrooms	price
0	2104	3	399900
1	1600	3	329900
2	2400	3	369000
3	1416	2	232000
4	3000	4	539900

归一化

因为房屋面积和卧室数量以及售价的数字大小差距过大，为防止相应线性参数大小差距也过大，通过归一化将他们缩放到相同量级进行运算，只需最后还原即可

def normalize_feature(data):
    return (data-data.mean())/data.std()
data=normalize_feature(data)
data.head()

	size	bedrooms	price
0	0.130010	-0.223675	0.475747
1	-0.504190	-0.223675	-0.084074
2	0.502476	-0.223675	0.228626
3	-0.735723	-1.537767	-0.867025
4	1.257476	1.090417	1.595389

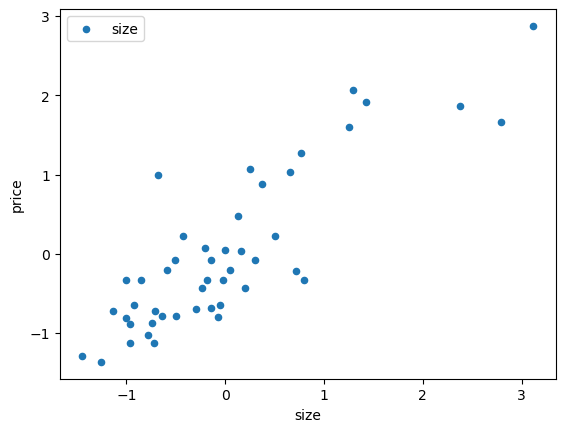
1 2	data.plot.scatter('size','price',label='size') plt.show()

png

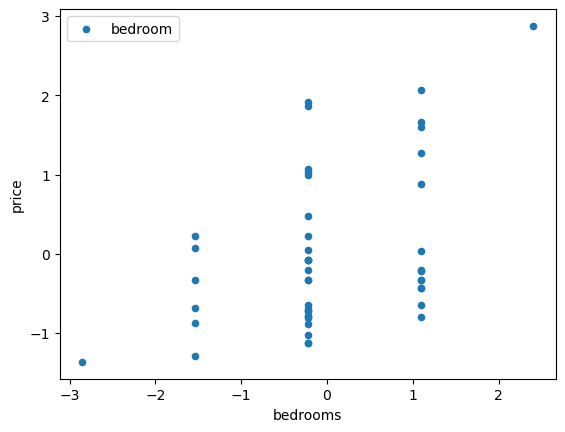
1 2	data.plot.scatter('bedrooms','price',label='bedroom') plt.show()

png

1 2	data.insert(0,'ones',1) data.head()

	ones	size	bedrooms	price
0	1	0.130010	-0.223675	0.475747
1	1	-0.504190	-0.223675	-0.084074
2	1	0.502476	-0.223675	0.228626
3	1	-0.735723	-1.537767	-0.867025
4	1	1.257476	1.090417	1.595389

X=data.iloc[:,0:-1]
y=data.iloc[:,-1]

X.head()

	ones	size	bedrooms
0	1	0.130010	-0.223675
1	1	-0.504190	-0.223675
2	1	0.502476	-0.223675
3	1	-0.735723	-1.537767
4	1	1.257476	1.090417

y.head()

0    0.475747
1   -0.084074
2    0.228626
3   -0.867025
4    1.595389
Name: price, dtype: float64

1 2	X=X.values X.shape

(47, 3)

1
2
3

y=y.values
y=y.reshape(47,1)
y.shape

(47, 1)

构造损失函数

def costFunction(X,y,theta):
    inner=np.power(X@theta-y,2)
    return np.sum(inner)/(2*len(X))
theta=np.zeros((3,1))
cost_init=costFunction(X,y,theta)
print(cost_init)

0.48936170212765967

构造梯度下降

def gradientDescent(X,y,theta,alpha,iters):
    costs=[]
    for i in range(iters):
        theta=theta-alpha*(X.T@(X@theta-y))/len(X)
        cost=costFunction(X,y,theta)
        costs.append(cost)
        
    return theta,costs

alpha=[0.0003,0.003,0.03,0.0001,0.001,0.01]
iters=2000

fig,ax=plt.subplots()

for each in alpha:
    _,costs=gradientDescent(X,y,theta,each,iters)
    ax.plot(np.arange(iters),costs,label=each)
    ax.legend()
    
ax.set(xlabel='iters',ylabel='cost',title='cost vs iters')
plt.show()

png

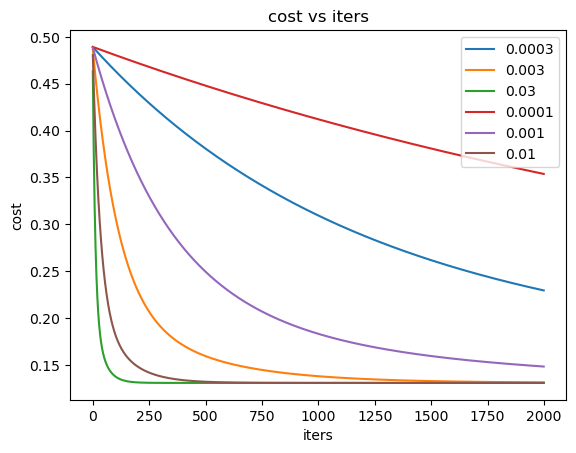
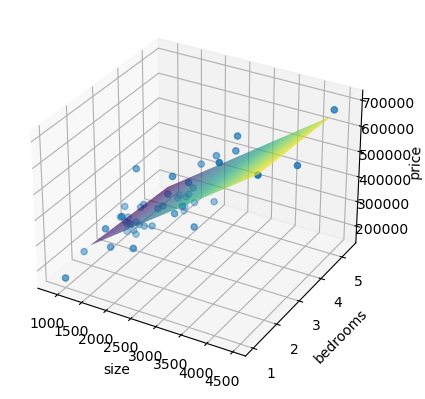
对结果进行归一化还原并画图

x=np.linspace(y.min(),y.max(),100)
x_s=x
x_b=x
x_s,x_b=np.meshgrid(x_s,x_b)
y_=_[0,0]+_[1,0]*x_s+_[2,0]*x_b

y_=y_*(data_2.iloc[:,2].std())+(data_2.iloc[:,2].mean())
x_s=x_s*(data_2.iloc[:,0].std())+(data_2.iloc[:,0].mean())
x_b=x_b*(data_2.iloc[:,1].std())+(data_2.iloc[:,1].mean())

fig=plt.figure()
ax=fig.add_subplot(111,projection='3d')
ax.scatter(data_2.iloc[:,0],data_2.iloc[:,1],data_2.iloc[:,2])
ax.plot_surface(x_s, x_b, y_, rstride=1, cstride=1, cmap='viridis', edgecolor='none')
ax.set_xlabel('size')
ax.set_ylabel('bedrooms')
ax.set_zlabel('price')
plt.show()